Relations and Functions
In programming, we often deal with paired data:
- username — email
- person — phone number
- id — company
All cases can be considered as two sets, with a rule to connect their elements. Given two sets A and B, a map function f from A to B, denoted as
f: A \rightarrow B
is an assignment to each element a in A of a single element in B.
We sometimes use a notation a \mapsto f(a) (note the different arrow) to indicate that a maps to some value via function f. We call f(a) an image of a. Set A is called the domain of f, and B the codomain of f.
Notice how we talk about functions as static data, not as a process. In programming, we’re used to functions being descriptions of processes, even though in most languages we can pass functions around as data. But consider this: how would you cache a function call? An obvious approach is to pre-compute some answers beforehand and store them in a table:
| Argument | Return |
|---|---|
| “a” | 52321 |
| “b” | 12321 |
| "c | 81872 |
| … | … |
Theoretically, we could do this for all possible arguments, which would allow us to disregard all function’s code and continue operating with a cache table exclusively. This means that any function (unless it deals with randomization) can be represented as static data. A mathematical notation of a function as a relation between two sets (essentially, a set of arguments and a set of return values) generalizes this idea.
A binary relation of two sets A and B is a subset of A \times B. (Recall that A \times B is a set of all combinations of pairs of values of the two sets). Thus, a function is a binary relation, having the property that for each element a \in A there is exactly one ordered pair in A \times B whose first component is a. There are three types of relations:
1. The function f: A \rightarrow B is one-to-one (injective) if no two values of A result in the same value of B. In other words, there’s at most one incoming arrow for each element of B. Formally: for any two distinct elements a and a' in A, we have f(a) \neq f(a').
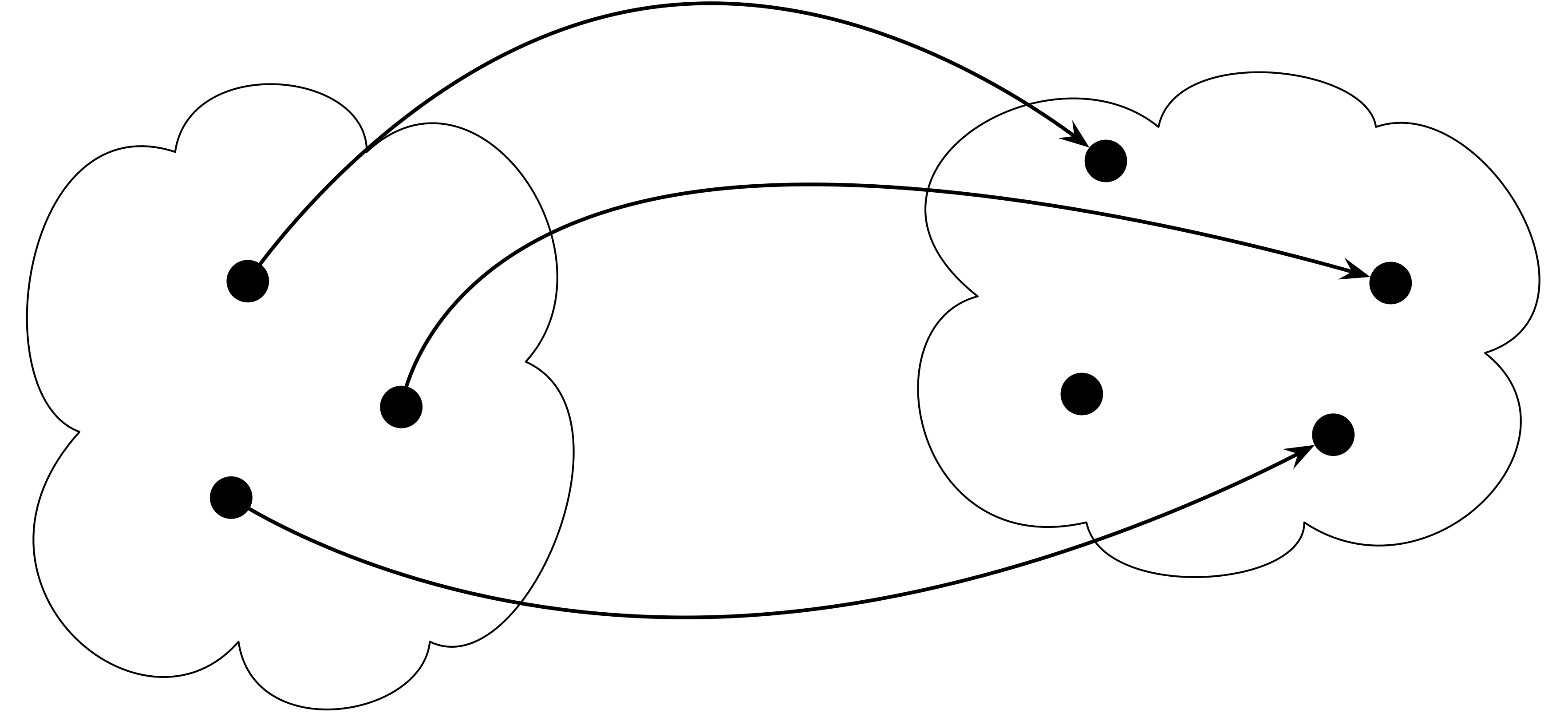
2. The function f: A \rightarrow B is onto (surjective) if all elements of B are covered. In other words, no element of B is without at least one arrow. Formally: for each element b \in B, there exists an element a \in A, such that f(a) = b.
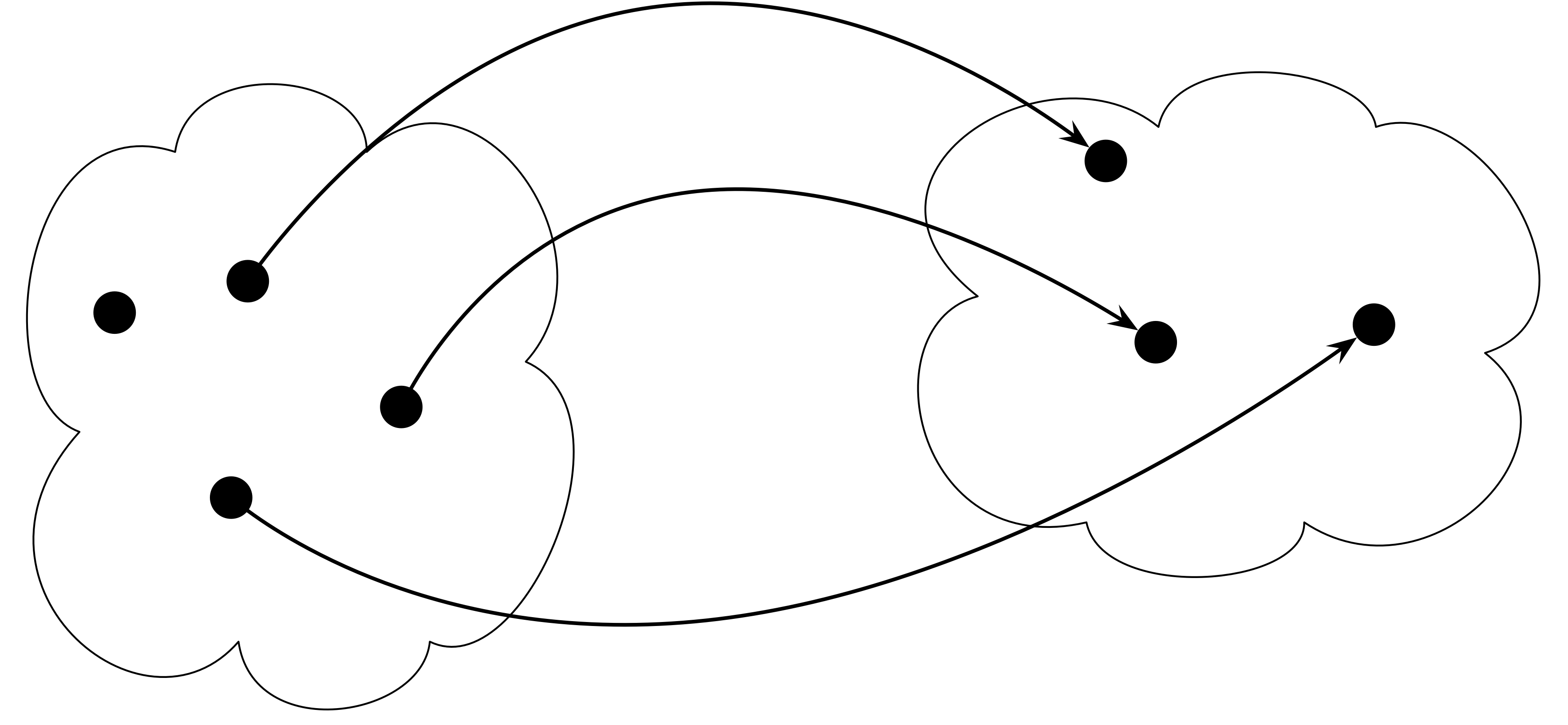
3. The function f is bijective if f is both injective and surjective. In other words, all elements of A are mapped uniquely to all elements of B.
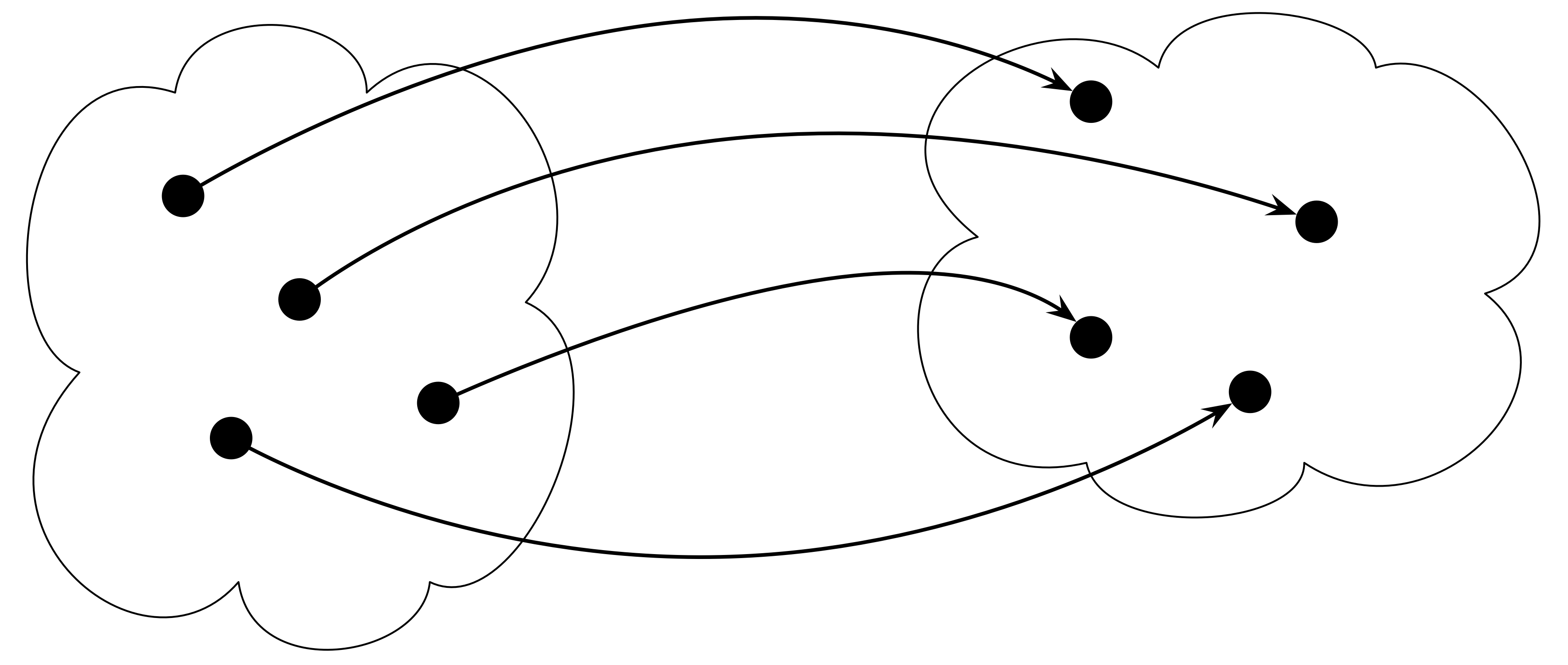
We’ll not focus on functions and relations anymore at the moment. Depending on how this course goes on, we’ll either keep getting back to elements of this topic, or will extract it into a separate chapter.